曲面建模講解與實例
很多人在討論軟件中的曲面建模方法,這其中包括NURBS、PATCH、SURFACE,和SUB DIVETION(細分)先介紹幾個連續**的概念,需小小的高數基礎,但為了讓我們更好地理解曲線建模,不要畏懼它!LET’S BEGIN 某節點兩端曲線在該點重合,則該點具有C0、G0級連續; 該點兩端曲線重合,切矢量方向相同,大小不等,稱為G1級連續, 該點兩端曲線重合,切矢量方向相同,大小相等,稱為C1級連續,如果兩端曲線重合,切矢量導數方向相同,大小不等稱為G2級連續,如果兩端曲線重合,切矢量導數方向相同,大小相等稱為C2級連續,至二階三階有C2、G2、C3、G3等連續方式。一般默認的NURBS(MAX中MAYA中)連續,是C23級別,控制點(CV、EP)的權重反映了切線的大小數值,而在高精度的工業設計中可應用于更高的連續級別。而把這些概念應用于BRZEIL上,我們可以看到,MAX中的BREZIL曲線可以較為自由地改變其節點連續**,將之轉化成CORNER形或是BREZIL CORNER,就是C0G0級別,將之轉成BEZIL形就是兩端曲線切線柄方向一致就是G1形,轉成SMOOTH,因切線柄兩端方向一致大小一致因此是C1形, 因為都屬于有理化樣條曲線,所以BREZEIL和NURBS之間是可以轉換的,也就是說PATCH和NURBS曲面是可以轉換的,所以正像前面說了,MAYA中NURBS面片建模的原理其實和PATCH原理極其相似,不過一般要滿足四邊面的拓樸關系,而PATCH也是一樣的,如果出現三角面,曲面的光滑度很難控制,像是A:M和MAX中的基于樣條曲建模手段,在MAX叫做SURFACE,其實也就連續**。細分是從多邊形和NURBS中演生出的一種建模手段,在MAX中叫做NURMS,可以用少量的點、線、面是PATCH的快速方法,類似的方法其實用NURBS也可以實現,比如說在RHINOS中可織成曲線網,然后用三邊線成面或四邊線成面并要注意其子物體控制曲面的形態,并可以調整其子物體上的權重WEIGHT。
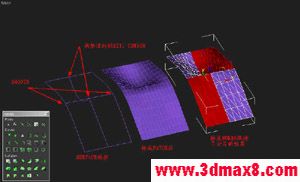 ??接下來是實例,初學者要掌握曲面建模技術,最主要的是要理解連續**的問題,也就是在轉折處有轉折,在平滑處有光滑,怎樣做到呢? 一般較為復雜的曲面最好不要由單獨一塊面片(NURBS或PATCH)生成,而要由分片來實現。 不過在這里我們不討論那么復雜的過程,我們來嘗試做一個鼠標.
1,繪出底線輪廓和幾條關鍵曲線,注意拐角方式,
??接下來是實例,初學者要掌握曲面建模技術,最主要的是要理解連續**的問題,也就是在轉折處有轉折,在平滑處有光滑,怎樣做到呢? 一般較為復雜的曲面最好不要由單獨一塊面片(NURBS或PATCH)生成,而要由分片來實現。 不過在這里我們不討論那么復雜的過程,我們來嘗試做一個鼠標.
1,繪出底線輪廓和幾條關鍵曲線,注意拐角方式,
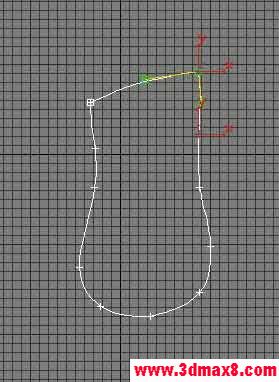 ??織網,在關鍵的轉折處可調整BREZIL桿來改變曲率大小,
??織網,在關鍵的轉折處可調整BREZIL桿來改變曲率大小,
 加了SURFACE修改器,將它改成鼠標,嗯,像個鼠標的樣子了。
加了SURFACE修改器,將它改成鼠標,嗯,像個鼠標的樣子了。
 可在PS中繪制貼圖
可在PS中繪制貼圖
 ??綜合應用UVW MAP和UNRAP UVW,這只是建模教程! 加上材質打上燈光,,渲染出圖.
??綜合應用UVW MAP和UNRAP UVW,這只是建模教程! 加上材質打上燈光,,渲染出圖.


 ??接下來是實例,初學者要掌握曲面建模技術,最主要的是要理解連續**的問題,也就是在轉折處有轉折,在平滑處有光滑,怎樣做到呢? 一般較為復雜的曲面最好不要由單獨一塊面片(NURBS或PATCH)生成,而要由分片來實現。 不過在這里我們不討論那么復雜的過程,我們來嘗試做一個鼠標.
1,繪出底線輪廓和幾條關鍵曲線,注意拐角方式,
??接下來是實例,初學者要掌握曲面建模技術,最主要的是要理解連續**的問題,也就是在轉折處有轉折,在平滑處有光滑,怎樣做到呢? 一般較為復雜的曲面最好不要由單獨一塊面片(NURBS或PATCH)生成,而要由分片來實現。 不過在這里我們不討論那么復雜的過程,我們來嘗試做一個鼠標.
1,繪出底線輪廓和幾條關鍵曲線,注意拐角方式,
 ??織網,在關鍵的轉折處可調整BREZIL桿來改變曲率大小,
??織網,在關鍵的轉折處可調整BREZIL桿來改變曲率大小,
 加了SURFACE修改器,將它改成鼠標,嗯,像個鼠標的樣子了。
加了SURFACE修改器,將它改成鼠標,嗯,像個鼠標的樣子了。
 可在PS中繪制貼圖
可在PS中繪制貼圖
 ??綜合應用UVW MAP和UNRAP UVW,這只是建模教程! 加上材質打上燈光,,渲染出圖.
??綜合應用UVW MAP和UNRAP UVW,這只是建模教程! 加上材質打上燈光,,渲染出圖.


贊
0












評論(5)